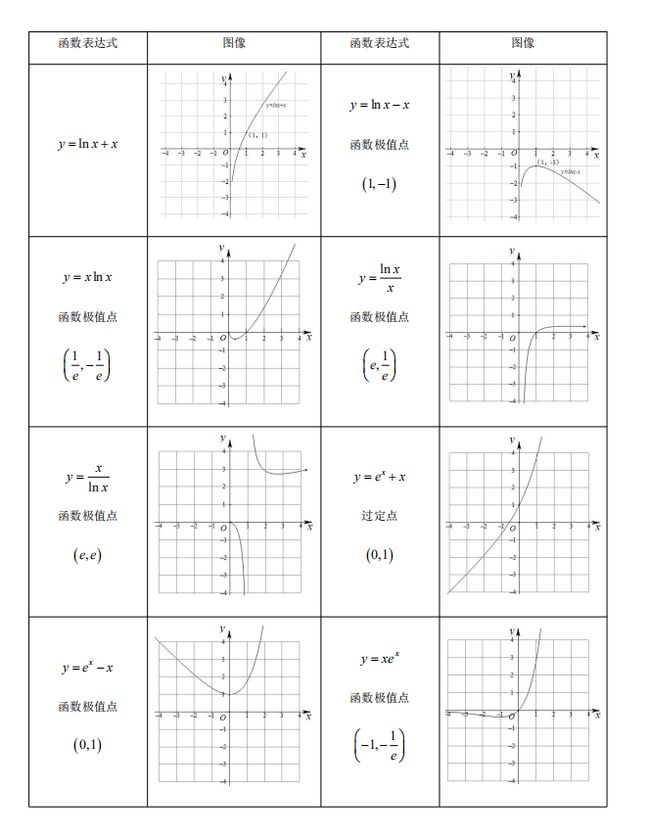
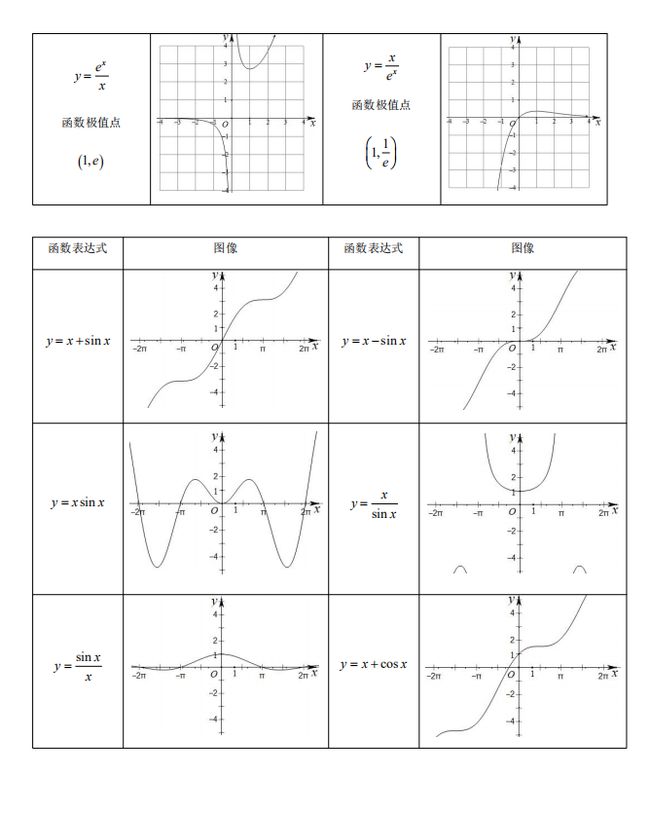
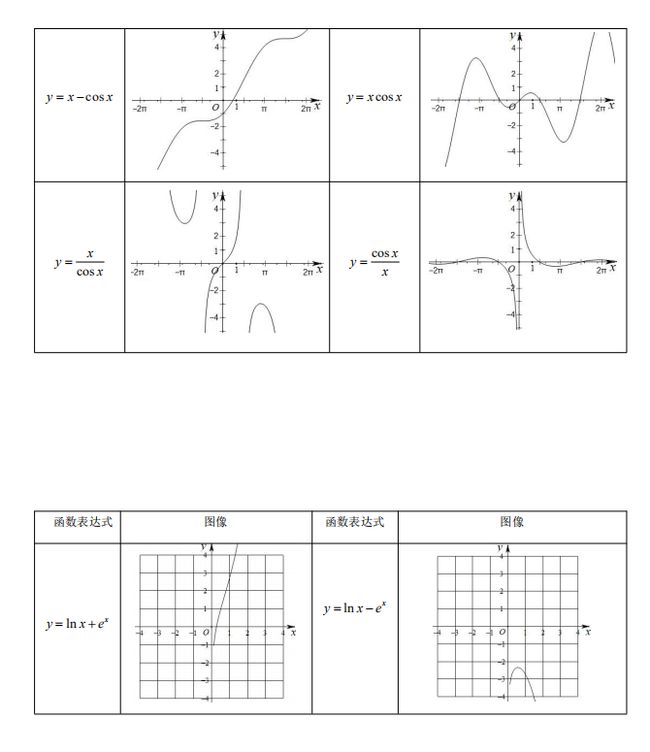
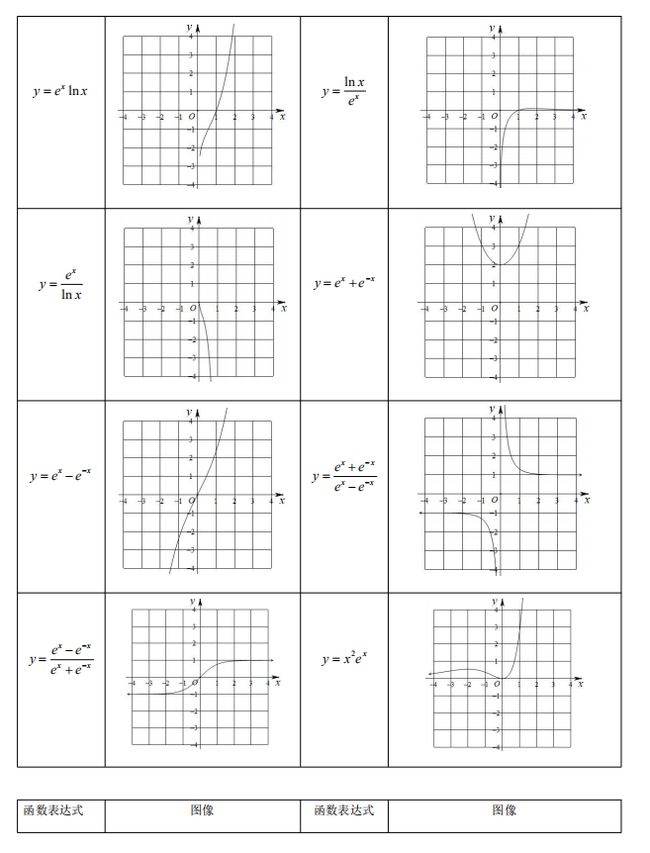
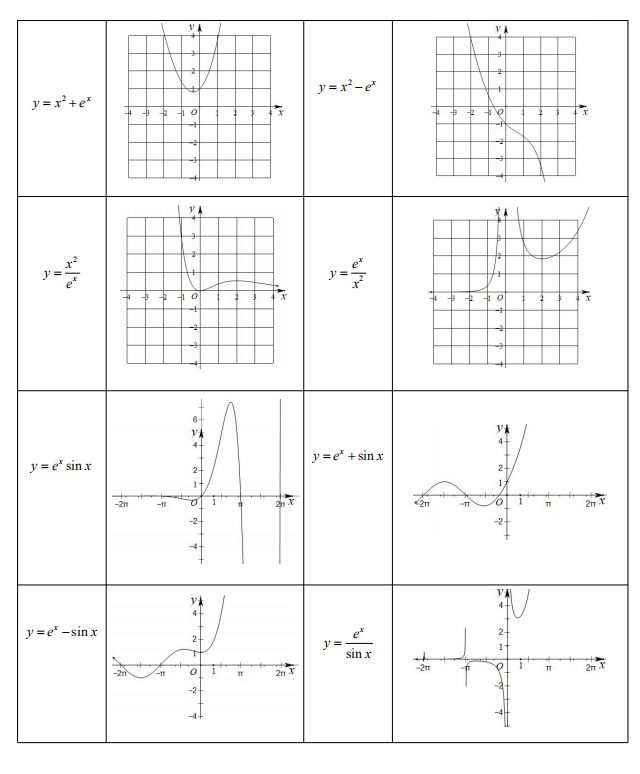
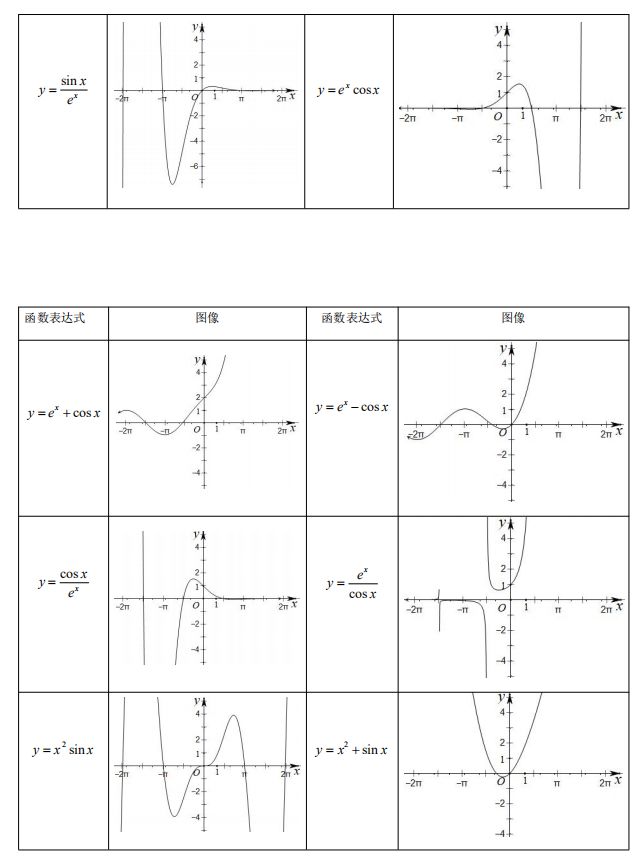
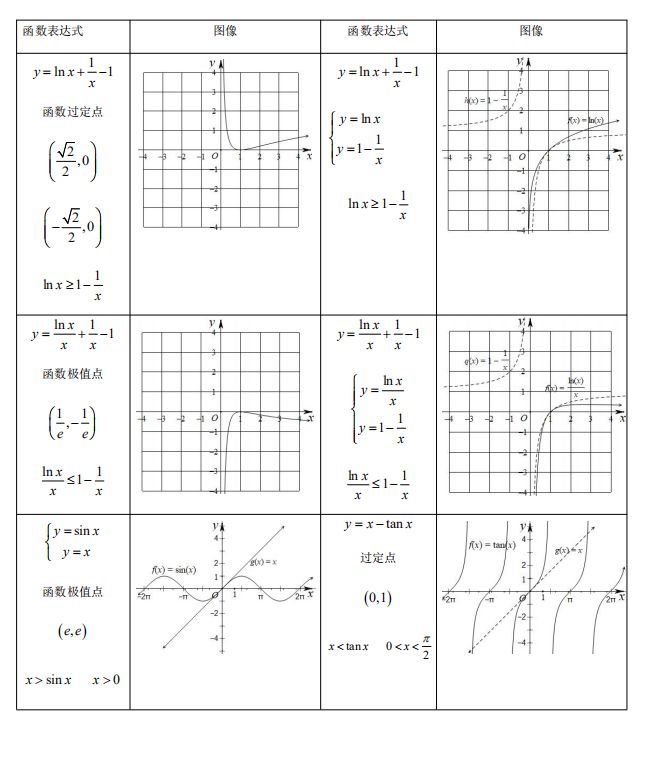
函数图象是函数的核心问题，高考主要考查函数图象的辨识与变换，考查函数图象的应用和运用函数图象理解和研究函数的性质，考查运用数形结合思想分析与解决问题的能力．在高考复习中要注意以下几点：

　　一、有关图象辨识问题

　　1.由实际情景探究函数图象．重要是将生活问题转化为我们熟悉的数学问题求解，要注意实际问题中的定义域问题．

　　2.利用动点探究函数图象．解决此类问题能够根据已知条件求出函数解析式后再推断函数的图象；也可采用“以静观动”，即将动点处于个别特殊的位置处考察图象的变动特征，从而作出挑选．

　　二、图象应用问题

　　1借助函数图象确定函数解析式，要注意综合应用奇偶性、单调性等相关性质，同时结合自变量与函数值的对应关系．

　　2.借助函数图象研究两函数图象交点的个数时，常将两函数图象在同一坐标系内作出，借助数形结合求解参数的取值范围．

　　3.借助函数的图象研究不等式 当不等式问题不能用代数法求解但其与函数有关时，常将不等式问题转化为两函数图象的上、下关系问题，从而借助数形结合求解．

　　4.借助函数的图象研究方程根的个数 当方程与基本函数有关时，能够通过函数图象来研究方程的根，方程f(x)＝0的根就是函数f(x)的图象与x轴交点的横坐标，方程f(x)＝g(x)的根就是函数f(x)与g(x)图象交点的横坐标．

　　期望给2021届的考生和家长带来帮助！

　　函数图像整整“62个”私信发送“函数62”我无偿发给你电子版！