黄冈市十校联考:2020~2021学年中考第一次模拟，数学考题与解析。

　　几何已占据半壁江山，思维与创新相交织，数形结合成为解题之葵花宝典！

　　看填空压轴题——

　　16.如图，一次函数的图象与x轴、y轴分别相交于A、B两点，将△AOB沿直线AB翻折，得到△ACB，若C的坐标为(3/2，√3/2)，则该一次函数的解析式为——。

　　

 

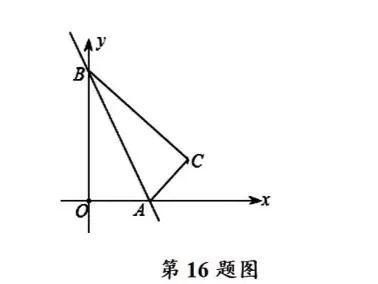
　　[分析]:求一次函数y=kx＋b的常规解法是，由A、B两点的坐标，借助待定系数法，得到关于k、b的二元一次方程，解出k、b的值即可。

　　对于本题，A、B的坐标未知，仅知C的坐标，而C又不在直线AB上，怎么根据C的坐标来求直线AB的方程呢？

　　

 

　　那就先求出A、B两点的坐标吧！

　　解:如上图，我们可过C作x轴的垂线，垂足为D，因C(3/2，√3/2)，则有CD=√3/2，OD=3/2(点的坐标的意义)。

　　由三角函数知识，知tan∠COD=CD/OD=√3/3，故∠COD=30°。

　　又连结OC与AB交于点E，则AB丄OC，OE=EC(O与C对称的结果)，故在Rt△AEO中，∠OAE=60°，从而，∠EAC=60°，进而∠CAD=60°，显然，在Rt△ADC中，∠ACD=30°，故AD/CD=tan∠ACD，即AD=tan30°CD=√3/3×√3/2=1/2，因此OA=ODーAD=3/2ー1/2=1，即A的坐标为(1，0)。

　　同理，在Rt△AOB中，OB=tan∠OAB×OA=tan60°×1=√3，即B的坐标为(0，√3)。

　　把A、B的坐标代入y=kx＋b，可得k=-√3，b=√3，即一次函数的解析式为y=-√3＋√3。

　　另解:借助在直角三角形中，30°所对的边是斜边的一大半，可知CD=OC/2=OE=EC=√3/2，在Rt△OEA中，OA=OE/cos30°=(√3/2)/(√3/2)=1，即A的坐标为(1，0)。

　　同理在Rt△AOB中，因OAB=60°，故OB=tan60°OA=√3，即B的坐标为(0，√3)，根据截距的意义，知b=√3。

　　由A、B的坐标，易知，一次函数的解析式为y=-√3x＋√3。