前面早已介绍了“向量的加法等同于高中物理中的矢量和”,能够按力、位移、求和的法则去求向量和。
这一章还有一个向量部分的重难点,就是“平面向量基本定理”,掌握向量的减法运算是充分理解“平面向量基本定理”的一个关键知识准备。但向量的减法不像向量的加法那么能够立即在高中物理中找到常见的状况。所以,向量的减法运算尽管也是教学中的重点,但却让 许多人感到有点晦涩难懂和难以掌握。
那样什么是向量的减法呢?

我们把求两个向量差的运算叫做向量的减法。
求向量的减法运算有哪些方法呢?主要有三种方法。
一、把向量的减法运算转化成向量的加法运算
因为向量的加法相对比较容易掌握,假如学生们早已对向量的加法运算掌握得特别好,而又实在掌握不了向量的减法运算法则时,不妨把向量的减法运算转换成向量的加法运算来解决。
根据教材中对向量减法的定义:“向量 向量 ”等于“向量 加上向量 的相反向量”。所以,我们做向量 与向量 的减法运算时,只须要做出 即可。
学生们在掌握了向量减法运算是向量加法的逆运算这个原理后,按照这个原理再去理解教材上向量减法运算的三角形法则就容易多了。
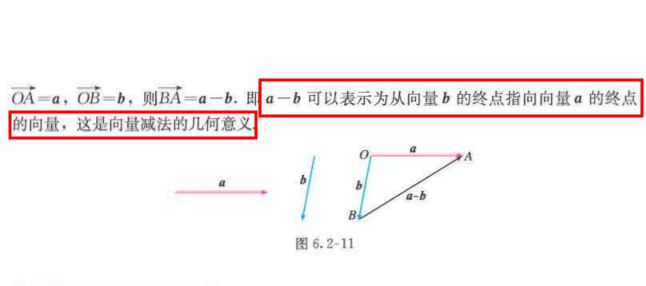
二、向量减法运算的三角形法则
借助相反向量,把向量的减法运算转换成向量的加法运算的原理,通过简单的作图后就能得到向量减法运算的三角形法则。向量减法的三角形法则有以下几个注意事项:
做减法的两个向量的起点重合(放在一起)。以“向量 向量 ”为例,要让 、 的起点重合。
向量减法的结果还是一个向量,并且这个结果对应的向量是从“减号后的向量终点指向减号前的向量终点”。

三、向量减法的“平行四边形法则”
根据向量减法的三角形法则的作图过程我们很容易能发现这么一个结论:
两个向量求和平行四边形法则做出的平行四边形中,和两个向量共起点的对角线向量是这两个向量的和向量。
不共起点的对角线所在的向量是这两个向量的差向量,两个向量中谁做“被减数”和谁做“减数”决定了这个对角线向量的指向。
以 为例,把 、 的起点放一起后借助向量加法的平行四边形法则做出平行四边形。和 、 不共起点的对角线所在向量表示的是 和 的差,并且 对应的平行四边形的对角线所在向量的方向,是从 的终点指向 的终点。
以上上是几何法求向量减法运算的三种方法,后面引入向量的坐标后还会学到向量减法的坐标运算。相对于目前用几何法求向量的减法运算,后面出现的向量减法的坐标运算就简单多了。
高一数学必修二 “向量的加法运算”知识点总结
高一数学必修二疑难点:向量的平行、共线、相等究竟是啥意思?